LeetCode의 Queue 튜토리얼에서 마지막 문제 Perfect Squares다.
Account Login - LeetCode
Level up your coding skills and quickly land a job. This is the best place to expand your knowledge and get prepared for your next interview.
leetcode.com
풀이를 보면 주로 DP를 사용하는 것 같은데 아직 거기까진 익숙하지 않기 때문에 그리고 지금은 Queue와 BFS를 풀이하는 중이기 때문에 차치하고 BFS를 활용하여 진행했다. 이번 문제는 풀이를 봐도 이해하는데 시간이 꽤 걸렸는데 다행히 Queue와 BFS를 사용하여 잘 설명된 풀이를 찾을 수 있었다. 뭐 결국은 스스로의 힘으로 풀지 못했다는 얘기다.
BFS and DP - LeetCode Discuss
Level up your coding skills and quickly land a job. This is the best place to expand your knowledge and get prepared for your next interview.
leetcode.com
이번 문제의 조건은 다음과 같다.
-
정수 n이 주어진다. n은 1 이상 10000 이하다.
-
가장 적은 개수의 Perfect Square Number를 합하여 n을 만들 수 있을 때 그 개수를 반환하라.
-
Perfect Square Number는 다른 정수의 제곱수를 의미한다(1, 4, 9 등).
어떻게 보면 간단한것 같으면서도 이런 문제는 처음이라 좀 난감했는데 이전처럼 큐를 활용하여 순차적으로 제곱수를 더하고 그걸 다시 큐에 삽입하면서 정수 n을 만들 때까지 반복하는 방식으로 이해할 수 있었다. 어쨌든 문제에서 요구하는 것은 정수 n을 만들기 위해 필요한 제곱수의 개수기 때문에 제곱수가 아닌 다른 수를 더할 이유는 없기 때문이다.
문제에서 예시로 주어진 12의 경우 4, 4, 4로 3개의 제곱수가 필요하며 13의 경우 9, 4로 2개의 제곱수가 필요하다. 그렇다면 이 제곱수를 어떻게 BFS로 탐색할 수 있을까? 일단 제곱수끼리의 합을 누적시킨다는 것에 주목할 필요가 있다.
언급했지만 이 문제에서는 모든 자연수가 아니라 제곱수만 합해서 주어진 값을 만들 수 있어야 한다. 그렇다면 제곱수끼리 합해가면서 주어진 값을 만들어보면 되지 않을까? 하지만 단순히 생각해서 1+4+9+... 처럼 더해나간다면 원하는 수를 찾기 힘들 것이다. 더하는 도중에 만들고자 하는 값을 넘어버릴 수도 있고 그럴 경우 지금까지 더한 수많은 제곱수 중에 뭘 빼야 하는지 알기 어려울 것이다.
그래서 이번 문제를 풀 때 사용되는 제곱수는 무조건 n 이하로, 정확히는 n에서 지금까지 누적된 제곱수를 뺀 값 이하로 제한해야 한다. 그래야 지금까지 누적된 제곱수와 새로 누적될 제곱수를 합해도 n을 초과하지 않을 것이다. 그렇다면 BFS 탐색을 적용할 경우 어떻게 누적을 시작해야 할까? 문제의 핵심은 누적이 0부터 시작한다는 것이다.
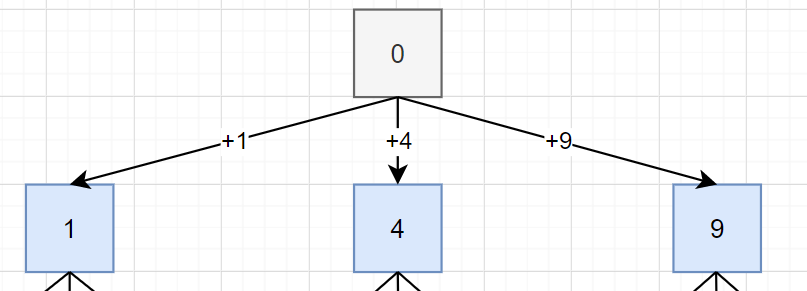
예시로 주어진 13을 탐색하는 과정을 살펴보자. 먼저 제곱수끼리만 더하기로 했으므로, 그리고 13을 초과하지 않아야 하므로 맨 처음에 누적할 수 있는 제곱수는 1, 4, 9가 있다. 맨 처음에 0으로 시작하기 때문에 BFS 탐색의 시작은 이 세 제곱수가 된다. 이들에 대하여 새로운 제곱수를 계속 누적시켜가면서 어느 순간 n을 완성시킨다면 해당 탐색이 몇 번째인지가 이 문제의 정답이 될 것이다. 그리고 이 누적된 제곱수를 기억하고 다음 탐색에서 다시 제곱수를 더해야 하기 때문에 이들을 큐에 삽입하여 BFS 탐색을 구현하는 것이다.
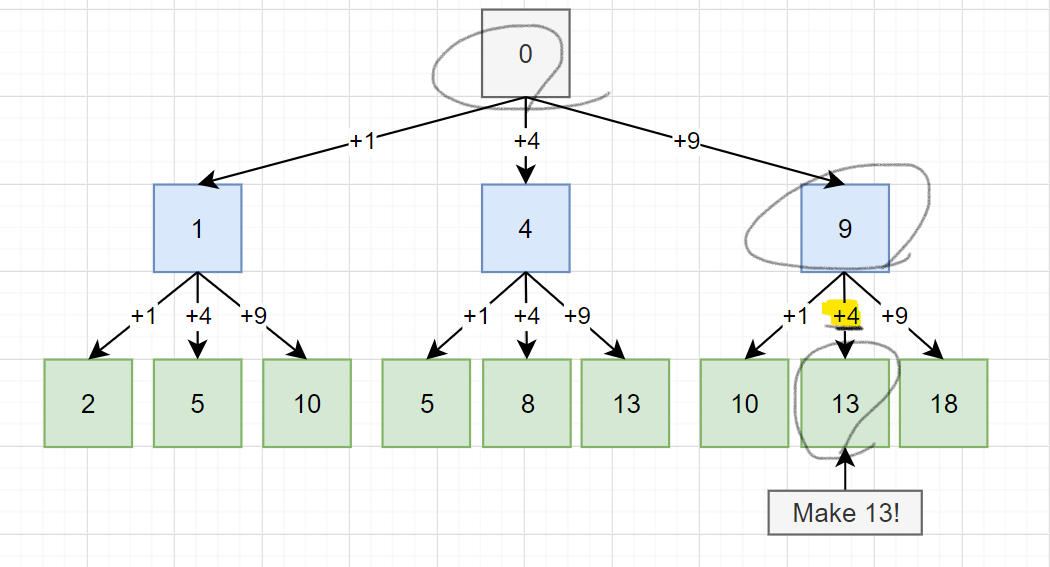
위의 예제의 경우 처음 제곱수 1, 4, 9에 대하여 각각 1, 4, 9를 누적시켜가면서 그 결과를 기준으로 판단하고 있다. 예를 들어 예제 13에서는 0에서 제곱수 9를 더하고 다시 제곱수 4를 더했을 경우 13이 완성된다. 이때 BFS 탐색은 두 번 실행되었기 때문에 총 두 개의 제곱수를 합하여 n을 만들 수 있다고 판단하는 것이다. 만약 누적된 제곱수가 아직 n보다 작다면 큐에 삽입하여 다음 탐색에서 이 누적된 제곱수에 새로운 제곱수를 합하면서 탐색하는 것이다.
만들어야 하는 값 n에 따라 얼마나 많은 제곱수의 합이 큐에 들어올지 모르기 때문에 모든 값을 꺼내서 순차적으로 제곱수를 누적시키고 다시 큐에 삽입해야 한다. 이전 문제와 마찬가지로 계산을 수행하기 전에 현재 큐에 포함된 아이템 갯수를 기억하여 원래 있던 제곱수들의 합만 빼낼 수 있도록 해야 한다.
제곱수끼리의 합을 구축하는 과정에서 예시의 12처럼 중복된 제곱수(4) 3개로 조합해야 하는 경우도 있어 중복은 문제가 되지 않는다. 하지만 2회 차 탐색 과정에서 다른 중복이 보이는데 바로 0 + 1 + 4와 0 + 4 + 1로 만들어진 제곱수들의 합 5다. 몇 개의 제곱수가 존재하든 어차피 다들 비슷한 제곱수끼리 더하기 때문에 이는 불필요한 연산이며 이미 계산된 값은 따로 저장해서 다시 계산하지 않도록 해야 한다.

이게 왜 중복되냐면 0 + 1 + 4나 0 + 4 + 1이나 순서만 바뀌었을 뿐 이 뒤로 누적되는 제곱수는 동일하기 때문이다. 위의 그림에서 볼 수 있듯이 둘 다 6, 9, 14라는 동일한 값으로 진행하는 것을 볼 수 있는데 이는 목표로 하는 수가 커질수록 중복이 발생할 확률도 커지며 기존에 계산했던 값을 또다시 계산하는 불필요한 일이 발생할 수 있다.
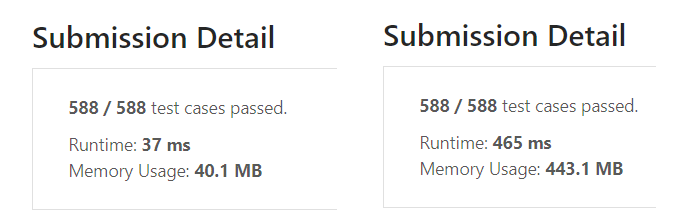
실제로 이를 기억하고 중복 계산을 생략하는 코드와 그렇지 않는 코드의 차이점을 보면 실행시간과 메모리 사용량이 약 10배로 어마어마하게 차이 나는 것을 볼 수 있다. 그렇기 때문에 HashSet 같은 자료구조를 사용하여 누적된 제곱수를 저장해야 다른 노드에서 누적된 제곱수를 계산하고 이미 계산된 값인 경우 더 이상 탐색하지 않는 로직을 적용해야 한다.
이를 바탕으로 구현된 코드는 다음과 같다.
import java.util.Queue;
import java.util.LinkedList;
import java.util.Set;
import java.util.HashSet;
class Solution {
public int numSquares(int n) {
Queue<Integer> queue = new LinkedList<Integer>();
Set<Integer> alreadyAddedSquareNumbers = new HashSet<Integer>();
int level = 0;
queue.add(0);
while(!queue.isEmpty()){
level++;
int previousLevel = queue.size();
for(int index = 0; index < previousLevel; index++){
int base = queue.poll();
for(int square = 1; square * square <= n - base; square++){
int sumOfSquares = base + square * square;
if(alreadyAddedSquareNumbers.contains(base + square * square) ||
sumOfSquares > n) continue;
if(sumOfSquares == n) return level;
else {
queue.add(sumOfSquares);
alreadyAddedSquareNumbers.add(sumOfSquares);
}
}
}
}
return -1;
}
}이미 계산된 제곱수들의 합을 기억하기 위해 alreadyAddedSquareNumbers라는 HashSet을 사용하고 있으며 각 탐색마다 회차를 기억하기 위해 level 변수를 사용하고 있다. 언급했듯이 제곱수부터 시작해야 하기 때문에 큐의 초기값은 0으로 주어진다. 그리고 큐에서 아이템, 즉 제곱수를 꺼내서 새로운 제곱수를 더하고 다시 큐에 추가하는 과정을 반복하는데 이때 큐에서 꺼낸 기존의 누적된 제곱수 값(base)과 새로운 제곱수(square * square)의 합이 찾고자 하는 값(n)을 넘어가면 의미가 없기 때문에 (square * square <= n - base)처럼 제한하고 있다.
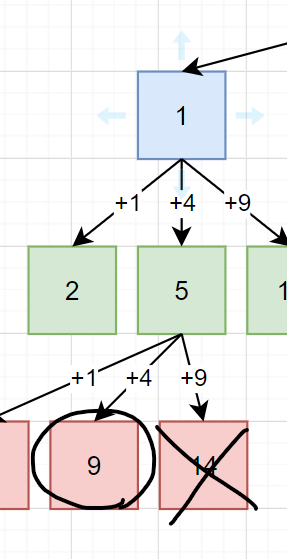
예를 들어 큐에서 꺼낸 누적값 base가 1 + 4 = 5고 새로 더할 제곱수 square * square가 3 * 3 = 9라고 할 때 우리가 찾아야 할 값 n이 13이라면 5 + 9는 14로 13을 초과하기 때문에 13 - 5 = 8을 넘는지 검사하여 초과하는 경우 계산하지 않는 것이다. 변수 square는 그냥 1부터 모든 제곱수를 더하기 위해 1 * 1, 2 * 2, 3 * 3,... 의 1, 2, 3으로 사용되는 값이다.
이렇게 새로 누적된 값이 아직 n에 미치지 못하고 중복된 계산 결과도 아니라면 다음 탐색에서 다시 제곱수를 더해보기 위해 큐에 삽입한다. 그리고 현재값을 alreadyAddedSquareNumbers에 추가하여 이미 계산됐다고 표시함으로써 큐에 남아있는 다른 제곱수의 누적값이 불필요한 계산을 하지 않도록 한다. 문제에선 주어지지 않은 조건이지만 큐에서 모든 누적 값들을 꺼내서 제곱수를 더했음에도 불구하고 n을 찾지 못했다면 -1을 반환한다.
이렇게 풀이를 작성하고 보면 Queue와 BFS를 사용하는 점에서 이전 문제와 유사한 구조를 보이고 있다. 단지 머릿속에는 아직 학부 시절에 배웠던 그래프에 적용하는 BFS, DFS만 남아있기 때문에 아직 고생중인데 나중에 문제를 더 풀면서 이런 고정관념을 바꿀 수 있으면 좋겠다. 말재주가 부족하여 내 머릿속에 있는걸 정확히 글로 옮기지 못했지만 필요한 사람에게 도움이 됐으면 좋겠다.
'알고리즘 > LeetCode' 카테고리의 다른 글
| Valid Parentheses (Stack) (0) | 2021.02.04 |
|---|---|
| Min Stack (Stack) (0) | 2021.02.04 |
| Open the Lock (BFS) (0) | 2021.02.03 |
| Number of Islands (DFS) (0) | 2021.02.03 |
| Number of Islands (BFS) (0) | 2020.07.21 |