이번 문제는 LeetCode의 Queue, Stack 튜토리얼에서 마지막 섹션의 첫 번째 문제인 Implement Queue using Stacks다.
이전에 학습할 때 큐와 스택의 가장 큰 차이점은 선입선출이냐 선입후출이냐의 차이였다. 즉 먼저 삽입된 요소가 먼저 삭제되거나 가장 나중에 삭제되는 완전 반대의 역할을 수행하고 있는데 스택을 이용하여 반대의 역할을 하는 큐를 구현할 수 있을까? 결론적으로는 가능하다. 하지만 추가적인 메모리 공간이 필요한데 일단 문제에서 요구하는 것은 다음과 같다.
-
구현된 큐는 push, pop, peek, empty 네 가지 연산을 수행할 수 있어야 한다.
-
큐를 구현할 때는 Stack 자료구조에서 지원하는 연산(push, pop, size, empty 등)만 사용해야 한다.
결과적으로 큐 자료구조를 구현한다고 해도 내부적으로는 스택을 사용하는 것을 원하는 것인데 1, 2, 3, 4를 삽입했을 때 가장 먼저 삭제되는 요소가 1이어야 한다는 것이다. 하지만 스택에서는 4밖에 삭제할 수 없는데 이를 어떻게 처리할 수 있을까? 이는 스택을 뒤집어서 저장하는 자료구조가 필요하다. 그래서 맨 처음 생각한 방법은 스택에 데이터를 삽입할 때마다 모든 데이터를 빼고 거꾸로 집어넣는 것이었다. 이는 다음과 같다.
import java.util.Stack;
class MyQueue {
int size = 0;
private Stack<Integer> stack = new Stack<>();
/** Initialize your data structure here. */
public MyQueue() {}
/** Push element x to the back of queue. */
public void push(int x) {
size++;
if(empty()){
stack.push(x);
return;
}
int[] buffer = new int[size - 1];
for(int index = 0; index < size - 1; index++){
buffer[index] = stack.pop();
}
stack.push(x);
for(int index = size - 2; index >= 0; index--){
stack.push(buffer[index]);
}
}
/** Removes the element from in front of queue and returns that element. */
public int pop() {
if(empty()) return -1;
size--;
return stack.pop();
}
/** Get the front element. */
public int peek() {
return stack.peek();
}
/** Returns whether the queue is empty. */
public boolean empty() {
return stack.empty();
}
}이는 스택 자료구조를 하나만 사용한 방법이지만 push 연산마다 동적 배열을 생성하여 모든 스택 요소를 pop 하여 저장한 후 삽입된 데이터를 스택에 삽입하고 배열에 있는 데이터를 다시 거꾸로 스택에 삽입하는 방식이다. 이때 스택의 크기 - 1 만큼 동적 배열을 생성하기 위해 따로 정수형 변수로 스택의 크기를 유지하고 있다.
위의 로직의 경우 만약 스택에 3, 2, 1이 삽입되어 있다면 여기에 4를 삽입할 때 스택에 있는 모든 요소를 꺼내 동적 배열에 1, 2, 3처럼 저장한 후 스택에 4를 삽입한다. 그리고 동적 배열에 있는 요소들을 거꾸로 참조하여 3, 2, 1 순서대로 스택에 삽입함으로써 결과적으로 스택에 4, 3, 2, 1을 삽입하게 된다.
이는 큐에서 삭제할 때 내부 스택의 pop 연산만 수행해주면 되기 때문에 간단하지만 큐에 요소를 삽입할 때 동적 배열을 생성해야 하는 등 부담이 너무 크다. 이를 좀 더 최적화할 순 없을까? 솔루션을 확인하니 두 개의 스택을 사용하는 방법으로 구현한 것을 볼 수 있었다. 두 개의 스택을 활용하는 방법은 또다시 두 개 의 방법으로 나뉘는데 이 스택을 큐로 전환하는 연산의 부담이 삽입 연산에 가해지는지, 삭제 연산에 가해지는지 차이다.
먼저 첫 번째 방법은 삽입 연산 때 부담이 가해지는 경우다. 먼저 두 개의 스택을 생성하는데 한 스택(s1)에는 기존에 삽입된 요소들이 저장되며 다른 스택(s2)은 위의 코드에서 동적 배열처럼 스택을 큐로 전환하는 연산 때 사용된다. 삽입 연산은 스택 s1에 있는 데이터를 모두 pop 해서 s2 스택에 push 한다. 그리고 삽입된 데이터를 스택 s1에 삽입하고 스택 s2에 있는 데이터를 다시 pop 해서 s1 스택에 push 한다. 이는 위에서 구현했던 것처럼 스택 s1에 [3, 2, 1]이 저장되어 있고 4를 삽입한다면 s2 스택에 [1, 2, 3]을 저장, s1 스택에 [4]를 저장, 그리고 s2 스택에 있는 요소들을 다시 s1 스택에 저장하여 [4, 3, 2, 1]이 저장된다. 동적 배열 대신 스택을 사용하기 때문에 따로 size 변수를 유지할 필요가 없다는 게 장점이다. 그리고 삭제 연산에서는 단순히 스택 s1에서 pop 연산을 수행하면 된다.
두 번째 방법은 삭제 연산 때 부담이 가해지는 경우다. 동일하게 두 개의 스택을 생성하지만 이전과는 달리 스택 s1에는 삽입된 데이터를 순서대로 저장한다. 대신 삭제 연산 시 스택 s1에 저장된 데이터들을 전부 스택 s2로 옮겨 담는다. 이때 스택 특성상 push, pop은 역순이기 때문에 스택 s2에는 거꾸로 담기게 된다. 그래서 스택 s2에서 pop만 해주면 데이터를 삭제(또는 반환)할 수 있는데 그럼 스택 s2에 있는 데이터를 다시 스택 s1에 옮겨 담아야 할까? 여기서는 그렇지 않고 스택 s2도 데이터들을 저장하는 공간으로 활용한다.
예를 들어 스택 s1에 [1, 2, 3, 4]처럼 데이터가 저장되어 있을 때 큐에서 데이터를 삭제하려면 스택에서 1을 삭제해야 한다. 하지만 현재는 일반적인 스택 순서대로 저장되어 있기 때문에 이를 뒤집기 위해 스택 s1에 저장된 데이터를 스택 s2에 옮겨 담는다. 그러면 스택 s2에는 [4, 3, 2, 1]처럼 데이터가 저장되어 있으며 여기서 맨 마지막 요소인 1을 반환한다. 그리고 데이터를 한번 더 삭제하면 어떨까? 이때는 스택 s2에 저장된 데이터를 삭제하면 된다. 굳이 s2에 저장했던걸 s1으로 다시 옮기지 않고 삭제 전용으로 사용하는 것인데 만약 삭제 연산으로 스택 s2에 있는 모든 데이터를 삭제했다면 이전에 했던 것처럼 스택 s1의 데이터들을 거꾸로 뒤집어 스택 s2에 저장한다.

큐는 삽입된 요소들을 순차적으로 삭제해야 하기 때문에 스택 s2에 저장된 데이터들을 그냥 순차적으로 pop 해주면 된다. 데이터를 삽입할 때도 스택 s2에 순차적으로 삽입해주다가 스택 s2에 있는 모든 데이터를 pop 해서 더 이상 삭제할 데이터가 없다면 그때 스택 s1에 저장된 데이터들을 스택 s2로 불러들여서 뒤집어서 다시 삭제 연산으로 제공하는 것이다.
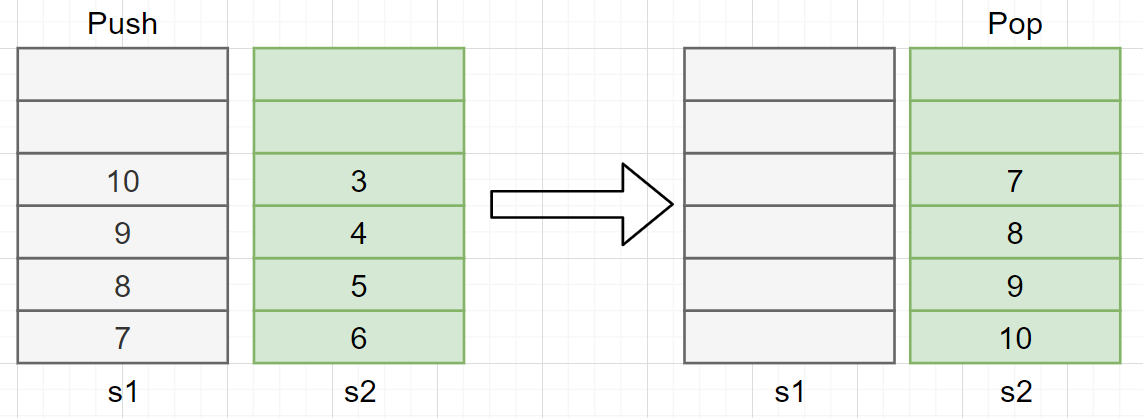
위의 그림처럼 스택 s2에서는 삭제를, 스택 s1에서는 삽입을 담당하기 때문에 삭제 연산을 할 때는 3, 4, 5, 6 순서대로 반환되며 스택 s2가 비어있으면 스택 s1에 저장된 데이터를 pop 해서 스택 s2에 push 하는 방법으로 뒤집어서 저장, 다시 7, 8, 9, 10 순서대로 반환할 수 있는 것을 볼 수 있다.
그런데 이 경우 peek 연산을 수행하기가 좀 까다로울 수 있는데 스택 s2가 비어있지 않다면 그냥 스택 s2에 peek 연산을 수행한 값을 돌려주면 되지만 비어있다면 어떻게 참조할 수 있을까? 필요할 때마다 스택을 뒤집어볼 순 없으니 좋은 방법은 변수를 하나 유지해두고 스택 s1에 데이터가 삽입될 때 스택 s1의 첫 데이터라면 이를 변수에 저장해서 기억해두는 것이다. 예를 들어 1, 2, 3, 4를 삽입했을 때 스택 s1의 첫 데이터는 1이며 FIFO 자료구조인 큐 특성상 첫 데이터가 반환될 것이기 때문에 peek 연산 값은 이 첫 데이터가 맞다.

그렇지만 삭제 연산이 일어나서 스택 s1에 있는 데이터들이 스택 s2로 옮겨갔다면, 즉 스택 s2가 비어있지 않다면 스택 s1에서 저장한 변숫값은 무시하고 스택 s2의 peek 연산 결과를 우선으로 해야 한다.

위의 경우에서 스택 s1에 저장된 1, 2, 3, 4는 스택 s2에서 4, 3, 2, 1로 넘어갔기 때문에 스택 s1은 비어있었을 것이다. 거기서 5, 6, 7, 8, 9가 삽입되었기 때문에 변수에는 5를 저장하지만 실제로 큐에 대해 peek 메서드를 호출하면 스택 s2가 비어있지 않기 때문에 스택 s2의 peek 메서드 값을 반환해줘야 하는 것이다. 그리고 스택 s2가 비어있다면 굳이 스택 s1를 스택 s2로 옮길 필요 없이 변수에 저장된 스택 s1의 첫 데이터 값을 반환해주면 된다.
또 중요한 것은 데이터들이 두 개의 스택에 걸쳐서 저장되어 있기 때문에 큐가 비어있는지 확인하려면 두 스택이 모두 비어있는지 확인해야 한다.
만약 peek이든 pop이든 스택 s2가 비어있을 때마다 스택 s1에 있는 데이터들을 옮겨온 후 스택 s2를 peek 해주면 이런 방법을 사용하지 않아도 되겠지만 peek 연산 자체의 속도를 높이기 위해 이렇게 구축한 것 같다. 이 내용들을 바탕으로 다시 작성한 코드는 다음과 같다.
import java.util.Stack;
class MyQueue {
int front;
private Stack<Integer> stack = new Stack<>();
private Stack<Integer> reverseStack = new Stack<>();
/** Initialize your data structure here. */
public MyQueue() {
}
/** Push element x to the back of queue. */
public void push(int x) {
if(stack.empty()) front = x;
stack.push(x);
}
/** Removes the element from in front of queue and returns that element. */
public int pop() {
if(reverseStack.empty()){
while(!stack.empty()){
reverseStack.push(stack.pop());
}
}
return reverseStack.pop();
}
/** Get the front element. */
public int peek() {
if(!reverseStack.empty()){
return reverseStack.peek();
} else {
return front;
}
}
/** Returns whether the queue is empty. */
public boolean empty() {
return stack.empty() && reverseStack.empty();
}
}stack, reverseStack이라는 두 개의 스택을 활용하였으며 큐에 데이터를 삽입할 때는 stack(스택 s1)에 삽입한다. 이때 peek 메서드에서 사용하기 위해 맨 처음 요소를 front 변수로 유지해주고 데이터를 push 한다. 그리고 큐에서 데이터를 삭제할 때는 reverseStack(스택 s2)가 비어있다면 stack에서 모든 데이터를 꺼내와 reverseStack에 저장하고 reverseStack의 pop 메서드 호출 결과를 반환한다. 만약 reverseStack이 비어있지 않다면 그냥 pop만 해주면 될 것이다.
위에서 언급한 것처럼 큐의 공백 여부를 확인할 때는 두 스택이 모두 비어있는지 확인하고 peek 메서드는 reverseStack이 비어있다면 front 변숫값을 반환해주고 그렇지 않다면 reverseStack의 peek 메서드 호출 값을 반환해준다.
쉽게 생각했지만 생각보다 배울 점이 많은 문제였다. 동적 배열보다는 스택을 두 개 쓰는 게 더 깔끔한 것 같은데 실제로 스택으로 큐를 구현할 일은 없겠지만 LIFO, FIFO에 좀 익숙해지는 계기가 되었다.
'알고리즘 > LeetCode' 카테고리의 다른 글
| Decode String (Stack) (0) | 2021.02.11 |
|---|---|
| Implement Stack using Queues (0) | 2021.02.11 |
| Binary Tree Inorder Traversal (Stack) (0) | 2021.02.10 |
| Target Sum (DFS) (0) | 2021.02.09 |
| Clone Graph (DFS) (0) | 2021.02.09 |