LeetCode의 Binary Tree 튜토리얼의 두 번째 섹션의 첫 번째 문제인 Maximum Depth of Binary Tree다.
Explore - LeetCode
LeetCode Explore is the best place for everyone to start practicing and learning on LeetCode. No matter if you are a beginner or a master, there are always new topics waiting for you to explore.
leetcode.com
이진트리의 높이(또는 깊이)를 구하는 문제로 루트 노드부터 시작해서 가장 깊은 곳에 있는 자식 노드까지 몇 개의 노드를 거쳐가야 하는지 구하는 문제다. LeetCode의 Binary Tree 튜토리얼에서는 이런 문제의 전형적인 해법으로 재귀 함수를 이용한 Top-down, Bottom-up 방식을 제안했다.

일단 트리의 높이를 구하는 문제는 위의 그림과 같다. 루트 노드부터 시작해서 모든 자식 노드를 검사하며 가장 깊은 곳에 있는 자식 노드까지 도달했을 때 거친 노드의 개수가 트리의 높이가 되는 것이다. 위의 그림에서는 노드 1, 노드 3, 노드 4, 노드 6을 탐색하면 최대 높이인 4가 나오기 때문에 이 트리의 높이가 4라고 판단할 수 있다.
그렇다면 이렇게 가장 깊은 곳에 있는 노드는 어떻게 탐색할 수 있을까? 일단 루트 노드에서는 현재 전체 트리의 구조를 모르기 때문에 모든 자식 노드를 살펴봐야 한다. DFS나 BFS로 살펴보면서 자식 노드가 있으면 있을 때마다 트리의 높이를 하나씩 높여가면서 측정하는 방법인데 이 경우 스택이나 큐를 사용하기보다 재귀 함수를 사용하면 훨씬 더 간단하게 풀 수 있다.

재귀 함수로 트리를 탐색하는 방법은 Top-down 방식과 Bottom-up 방식이 있다. 전자는 현재(top) 노드의 깊이가 지금까지 측정된 트리의 높이보다 큰지 비교하여 업데이트하고 아래(down)의 자식 노드에 대해서 재귀 호출하는 방식으로 진행된다.
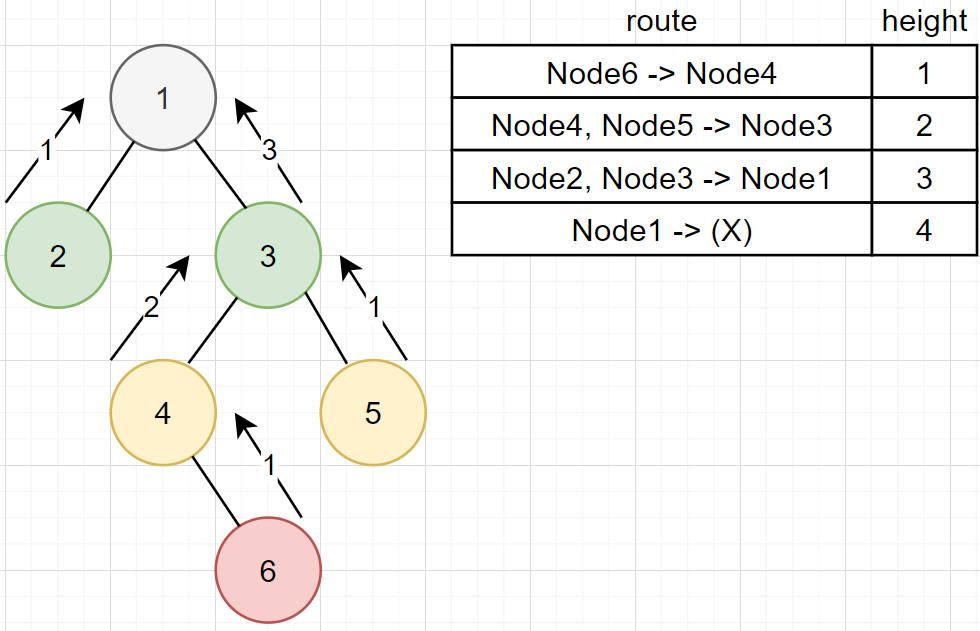
후자는 두 자식 노드에서 반환된 값 중 더 큰 값을 현재 노드부터 자식 노드까지의 높이로 측정하고 자신도 그 높이를 반환하는 방법인데 일단 두 자식 노드(bottom)를 재귀 호출한 후 그 결괏값이 다시 올라오기를(up) 기다린다는 점에서 bottom-up 방식이라고 할 수 있다.
탐색 함수를 재귀 호출하면서 풀 때는 현재 노드 높이에 1을 더한 값을 매개변수로 전달해서 트리에서 현재 노드의 깊이를 측정해야 한다. 이번 문제를 Top-down 방식으로 풀어보면 다음과 같다.
class Solution {
private int height = 0;
public int maxDepth(TreeNode root) {
if(root == null) return 0;
findDepth(root, 1);
return height;
}
public void findDepth(TreeNode node, int currentHeight){
if(height < currentHeight) height = currentHeight;
if(node.left != null) findDepth(node.left, currentHeight+1);
if(node.right != null) findDepth(node.right, currentHeight+1);
}
}확실히 재귀 호출이 더 간단한 것을 볼 수 있다. 그렇다면 Bottom-up 방식은 어떻게 구현할 수 있을까? 튜토리얼에서 언급한 알고리즘대로 구현하면 다음과 같다.
class Solution {
private int height = 0;
public int maxDepth(TreeNode root) {
if(root == null) return 0;
int height = findDepth(root);
return height;
}
public int findDepth(TreeNode node){
int leftHeight = 0;
int rightHeight = 0;
if(node.left != null) leftHeight = findDepth(node.left);
if(node.right != null) rightHeight = findDepth(node.right);
return leftHeight > rightHeight ? leftHeight+1 : rightHeight+1;
}
}현재 노드에서 왼쪽 자식 노드, 정확히는 왼쪽 서브 트리의 높이와 오른쪽 자식 노드, 역시 오른쪽 서브 트리의 높이를 비교해서 더 큰 쪽에 1을 더해서 반환하고 있다. 1을 더하는 이유는 현재 노드까지 포함한 높이를 반환하기 위해서다.
'알고리즘 > LeetCode' 카테고리의 다른 글
| Path Sum (Recursive) (0) | 2021.02.18 |
|---|---|
| Symmetric Tree (Recursive) (0) | 2021.02.18 |
| Group Anagrams (0) | 2021.02.17 |
| Most Common Word (0) | 2021.02.17 |
| String to Integer (atoi) (0) | 2021.02.16 |